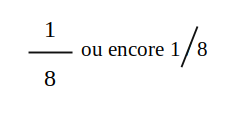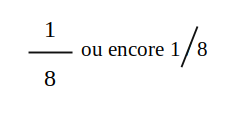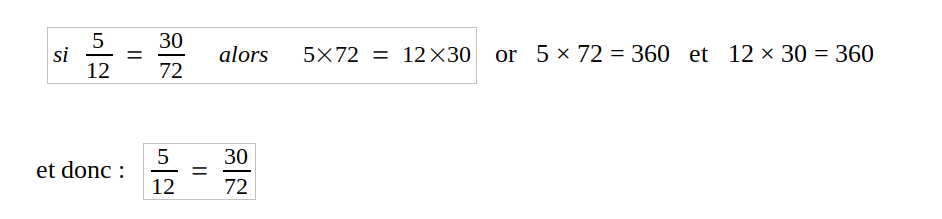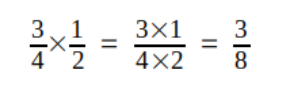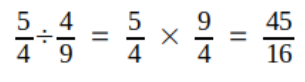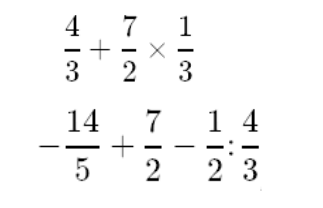LES FRACTIONS
1. Définition
- Une fraction est une portion (une partie, un morceau) d'un ensemble
- Par exemple, si des tartes sont partagées en 8 parts égales alors chaque part est un huitième d'une tarte, on le note :
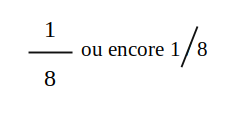
- Si je prends 3 parts d'une tarte, on dira que j'ai pris les trois huitièmes d'une tarte


- Si je prends 8 parts alors j'aurai pris huit huitièmes (8/8) de tarte, c'est à dire la tarte complète (8/8 = 1)
- Si je prends 11 parts alors j'aurai pris onze huitièmes (11/8) de tarte, c'est à dire une tarte complète plus 3 parts d'une autre tarte (11/8 = 1,375 >1 donc plus d'une tarte)
Exemples
- Une épreuve de course à pied s'effectue sur une distance de 12 km, lorsqu'un coureur a parcouru 5 km, il a effectué les cinq douzièmes de la course (5/12)
- Un bidon a une contenance de 45 litres, si je verse 5 litres à l'intérieur, il sera rempli aux cinq quarante-cinquièmes (5/45)
- Un moteur tourne à 60 tours/min au lieu de 100 tours/min, ce moteur tourne donc aux soixante centièmes (60/100) de sa capacité, comme le dénominateur est égal à 100, on pourra dire 60 pour 100 (60%) de sa capacité
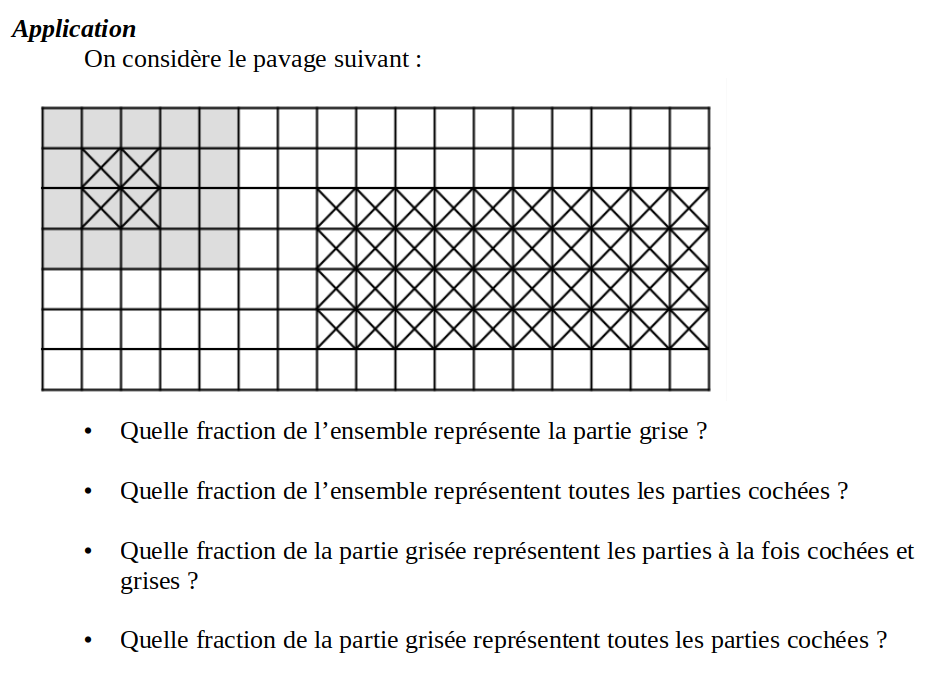
Réponses
Remarques
- Pas de nombre à virgule dans une fraction
- On ne laisse pas de nombre négatif au dénominateur
- Exemple 1 : 7/(-3) devient -7/3
- Exemple 2 : -8/(-3) devient 8/3 (règle des signes)
- Une fraction peut toujours se calculer
- Exemple 1 : -7/2 = -3,5
- Exemple 2 : 13/7 ≈ 1,857142857... on ne peut avoir qu' une valeur approchée, il est plus exact de travailler avec la fraction
- Un nombre relatif peut toujours s'écrire sous forme de fraction : le dénominateur vaut 1
2. Égalité entre deux fractions
Si deux fractions sont égales alors le produit du numérateur de la première et du dénominateur de la seconde est égal au produit du numérateur de la seconde et du dénominateur de la première

Exemple : vérification que 5/12 est bien égal à 30/72 :
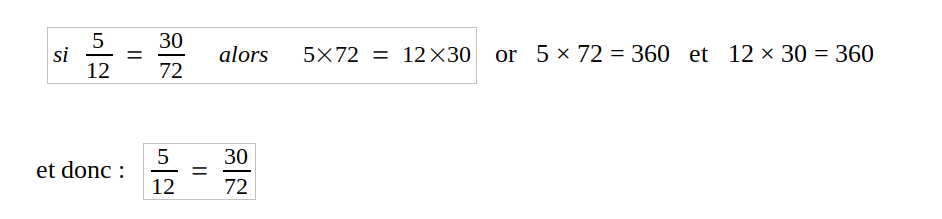

Réponse
3. Inverse d'une fraction
L'inverse d'une fraction est obtenu simplement en inversant le numérateur et le dénominateur
- Exemple 1 : 3/5 est l'inverse de 5/3
- Exemple 2 : -7/15 est l'inverse de 15/(-)7 que l'on note -15/7
- Exemple 3 : 1/4 est l'inverse de 4 (se souvenir que 4 = 4/1)
4. Simplification des fractions
- Il est souvent plus facile de travailler avec des petits nombres qu'avec des grands,
on peut, pour cela, simplifier les fractions quand c'est possible :
- Exemple 1 : exemple de la tarte partagée en 8 parts égales, si je prends 2 parts, j'aurai pris 2 huitièmes (2/8) de la tarte,ce qui revient à 1 quart (1/4) de la tarte
- Exemple 2 : si un automobiliste a parcouru 60 km sur les 180 km qu'il avait à parcourir, alors il a effectué les soixante cent quatre-vingtièmes (60/180) de la distance, ou encore un tiers (60/180 = 1/3) de son parcours
- Exemple 3 : si 24 personnes sur 800 sont riches, cela signifie que vingt-quatre huit-centièmes de la population est riche ou encore que trois centièmes (24/800 = 3/100) de la population est riche, soit 3%
- Méthode de simplification : il faut diviser ou multiplier le numérateur et le dénominateur de la fraction par le même nombre pour obtenir une fraction plus simple mais égale
- Exemple 1 : pour simplifier 14/21 il suffit de diviser 14 et 21 par 7 :
14 ÷ 7 = 2 et 21 ÷ 7 = 3 et donc 14/21 se simplifie en 2/3
- Exemple 2 : pour simplifier 260/40 il suffit de diviser 260 et 40 par 10 :
260 ÷ 10 = 26 et 40 ÷ 10 = 4 et donc 260/40 se simplifie en 26/4
qui peut encore se simpifier en divisant par 2 :
26 ÷ 2 = 13 et 4 ÷ 2 = 2 et donc 260/40 se simplifie en 13/2

Réponses
5. Comparaison de fractions
Pour comparer deux fractions il faut les mettre au même dénominateur puis comparer les numérateurs


Réponses
6. Opérations sur les fractions
- Addition et soustraction
- Pour additionner ou soustraire deux fractions, on commence par les simplifier, puis il faut les mettre au même dénominateur ensuite additionner ou soustraire les nouveaux numérateurs
- Exemple : lundi j'ai lu 7/20 de mon livre et mercredi 15/100, quelle fraction de mon livre ai-je lu ?


Réponses
- Multiplication
- Pour multiplier deux fractions, on commence par les simplifier, puis il faut les multiplier ensemble les numérateurs et les dénominateurs
- Exemple : J'ai mangé les trois quarts de la moitié d'une tarte, quelle part de la tarte ai-je mangé ?
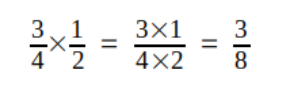

Réponses
- Division
- Pour diviser par une fraction, il suffit de multiplier par l'inverse de cette fraction
- Exemple :
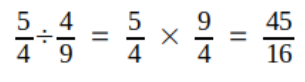

Réponses
- Applications - Calculer
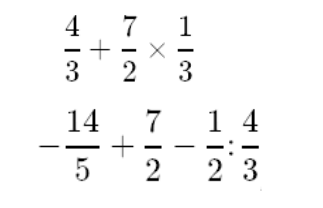
Réponses