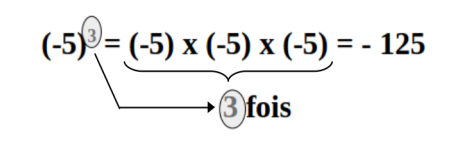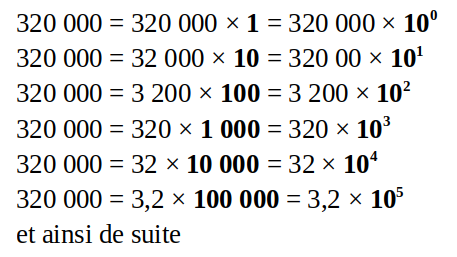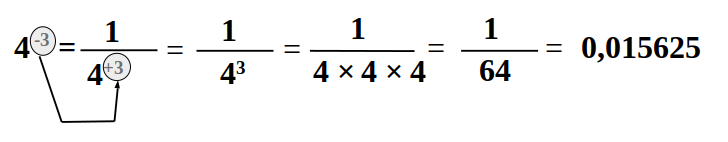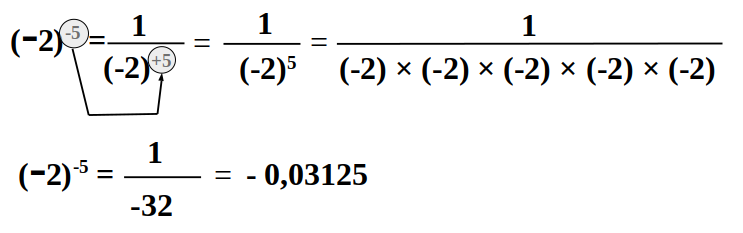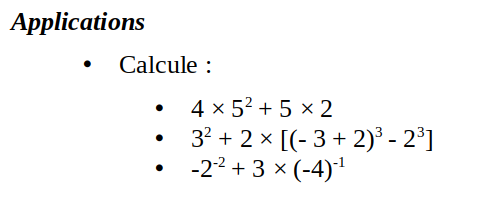LES PUISSANCES ENTIERES

1. Les puissances positives

1. Règle :

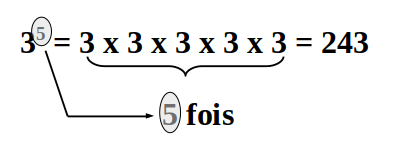
Un nombre A élevé à une puissance positive n est égal au produit AxAxAxA...xA,
il y autant de A que vaut n

• Exemple 1 :
  


• Exemple 2 :
  


• Exemple 3 : calcul du volume du pavé droit suivant :
  
  

  Le volume d'un pavé droit est donné par la formule longueur x largeur x hauteur
  Ce qui donne ici : Vol = 4m x 1,5m x 2m = 12 m x m x m = 12 m³




Remarque sur le rôle des parenthèses

Pour qu'un nombre négatif soit élevé à une puissance il faut que ce nombre soit entouré de parenthèses.
En effet - 3⁴ n'est pas égal à (-3)⁴ :

-3⁴ = - 3 x 3 x 3 x 3 = - 81
et (-3)⁴ = (-3) x (-3) x (-3) x (-3) = + 81


Sans la parenthèse, le signe n'est pas concerné par l'exposant




Cas particuliers

• Tout nombre élevé à la puissance 1 est égal à lui-même, ainsi : 5¹ = 5

• Tout nombre (sauf zéro) élevé à la puissance 0 est égal à 1, ainsi (-8)⁰ = 1


Réponses





2. Les puissances positives de 10 :

• Règle :
  Pour élever 10 à une puissance entière positive, il suffit d'écrire 1 suivi d'autant de zéros que l'indique la puissance
  

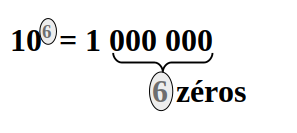
• Exemple :
  Quelques écritures possibles de 320 000 en utilisant les puissances positives de 10 :
  


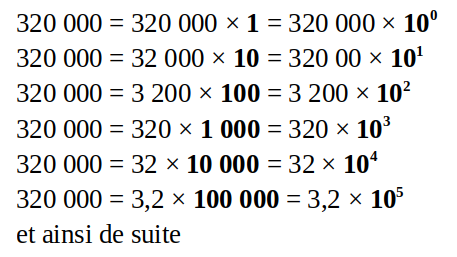
Réponses

2. Les puissances négatives

1. Règle :

Un nombre A (différent de zéro) élevé à une puissance négative -n est égal au quotient de 1 par A élevé à la puissance +n

• Exemple 1 :
  


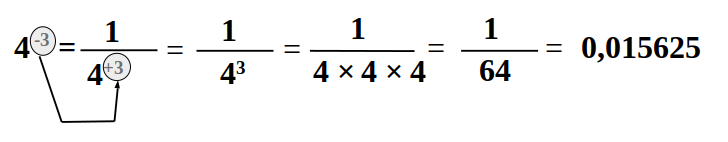
• Exemple 2 :
  



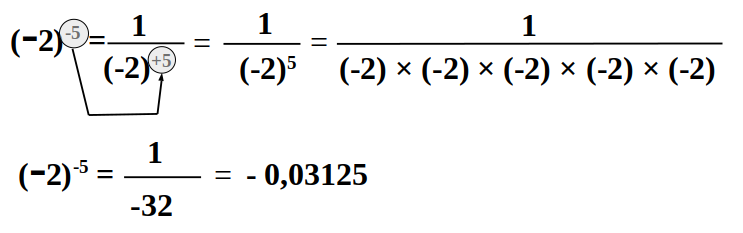
Réponses





2. Les puissances négatives de 10 :

• Règle :
  Pour élever 10 à une puissance entière négative, il suffit d'écrire autant de zéros que l'indique la puissance puis le chiffre 1,
  ensuite positionner la virgule juste après le premier zéro en partant de la gauche




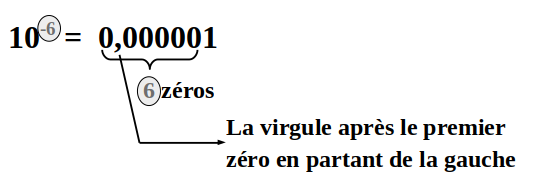
• Exemple :
  Quelques écritures possibles de 0,000654 en utilisant les puissances négatives de 10 :

  


Réponses

3. L'écriture scientifique d'un nombre

• Définition :
  
Un nombre est écrit en écriture scientifique s'il est constitué de la manière suivante :


± A x 10ⁿ avec 1 ≤ A < 10 et n un entier relatif

• Exemples :
  
• Exemple 1 :
  1254,4 s'écrit en écriture scientifique : 1,2544 x 10³


• Exemple 2 :
  - 0,0215 s'écrit en écriture scientifique : - 2,15 x 10^-2


Réponses

4. Les opérations avec les puissances

1. Multiplication


• Règle 1 : Aⁿ x A^m = A^n+m


• Exemple 1 :
  5³ x 5⁴ = 5³⁺⁴ = 5⁷ = 78125
  On vérifie : 5³ = 125 ; 5⁴ = 625 et 125 x 625 = 78125


• Exemple 2 :
  (-2)^-5 x (-2)⁴ = (-2)^-5+4 = (-2)^-1 = 1/(-2) = - 0,5
  On vérifie : (-2)^-5 = - 0,03125 ; (-2)⁴ = 16 et - 0,03125 x 16 = - 0,5


Remarque :
(-2)⁵ x (-2)^-5 = (-2)^5-5 = (-2)⁰ = 1
On vérifie : (-2)⁵ = -32 ; (-2)^-5 = -0,03125 et - 0,03125 x (-32) = 1
(-2)⁵ et (-2)^-5 sont dits inverses car leur produit est égal à 1


Réponses





• Règle 2 : (A x B)ⁿ = Aⁿ x Bⁿ


• Exemple 1 :
  5³ x 4³ = 125 x 64 = 8000
  On vérifie : (5 x 4)³ = 20³ = 8000


• Exemple 2 :
  (-2)^-5 x 5^-5 = - 0,03125 x 0,00032 = - 0,00001 = - 10^-5
  On vérifie : (-2 x 5)^-5 = (-10)^-5 = - 0,00001 = - 10^-5




Réponses





2. Division


• Règle : Aⁿ ÷ A^m = A^n-m


• Exemple 1 :
  5⁷ ÷ 5⁴ = 5^7-4 = 5³ = 125
  On vérifie : 5⁷ = 78125 ; 5⁴ = 625 et 78125 ÷ 625 = 125


• Exemple 2 :
  (-2)^-5 ÷ (-2)^-8 = (-2)^-5-(-8) = (-2)³ = - 8
  On vérifie : (-2)^-5 = - 0,03125 ; (-2)^-8 = 0,00390625
  et - 0,03125 ÷ 0,00390625 = - 8




Réponses





3. Puissance


• Règle : (Aⁿ)^m = A^nxm


• Exemple 1 :
  (5²)³ = 5^2x3 = 5⁶ = 15625
  On vérifie : 5² = 25 et 25³ = 15625


• Exemple 2 :
  ((-2)^-4)² = (-2)^-4x2 = (-2)^-8 = 0,00390625
  On vérifie : (-2)^-4 = 0,0625 et 0,0625² = 0,00390625




Réponses





4. Priorités dans une suite de calculs


• Règle :

Dans une suite de calculs, les opérations s'effectuent de la gauche vers la droite en respectant les priorités suivantes :
• D'abord les calculs entre parenthèses, en commençant par les parenthèses les plus intérieures
• Puis les puissances
• Ensuite les multiplications et divisions
• Enfin les additions et soustractions
• Exemple 1 : -3 + 3³ + 9 x (-2) - 24 : 2²
• D'abord les calculs entre parenthèses : ici il n'y en a pas !
• Puis les puissances : 3³ = 27 et 2^{2 = 4}
• Le calcul devient alors : -3 + 27 + 9 x (-2) - 24 : 4
• Ensuite les multiplications et divisions de gauche à droite : 9 x (-2) = -18 et 24 : 4 = 6
• Le calcul devient alors : -3 + 27 + (-18) - 6
• Enfin les additions et soustractions de gauche à droite
• -3 + 27 = 24 donc le calcul devient : 27 + (-18) - 6
• 27 + (-18) = 9 donc le calcul devient : 9 - 6 = 3
• Résultat : -3 + 3³ + 9 x (-2) - 24 : 2² = 3
• Exemple 2 : 8 - (-5 - (-8))² + 12 x 2^-2 - 2 - 8 x (-6 + 7)³
• D'abord les calculs entre parenthèses : (-5 - (-8)) = (-5 + (+8)) = 3 et (-6 + 7) = 1
• Le calcul devient alors : 8 - 3² + 12 x 2^-2 - 2 - 8 x 1³
• Puis les puissances : 3² = 9 ; 2^-2 = 1/2² = 1/4 et 1³ = 1
• Le calcul devient alors : 8 - 9 + 12 x 1/4 -2 - 8 x 1
• Ensuite les multiplications et divisions de gauche à droite : 12 x1/4 = 12/4 = 3 et 8 x 1 = 8
• Le calcul devient alors : 8 - 9 + 3 - 2 - 8
• Enfin les additions et soustractions de gauche à droite
• 8 - 9 = - 1 donc le calcul devient : -1 + 3 - 2 - 8
• -1 + 3 = 2 donc le calcul devient : 2 - 2 - 8
• 2 - 2 = 0 donc le calcul devient : 0 - 8 = - 8
• Résultat : 8 - (-5 - (-8))² + 12 x 2^-2 - 2 - 8 x (-6 + 7)³ = -8




Réponses