INTRODUCTION AUX ÉQUATIONS

1. Activité

Luc joue avec 1 balance à plateaux, 8 billes identiques de masse inconnue
et 7 dés de masse 15g.
Sa « mission » : poser sur chaque plateau des billes et des dés, obtenir l’équilibre
et ensuite trouver la masse d’une bille.

Après plusieurs tentatives, il trouve l’équilibre suivant :

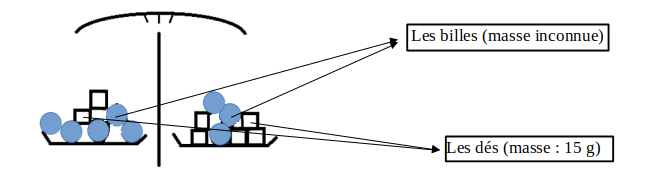
• Combien y a-t-il de billes et de dés sur chaque plateau ?

  Plateau 1 : 5 billes et 2 dés
  Plateau 2 : 3 billes et 5 dés
  



• Les deux plateaux de la balance sont à l’équilibre, ce qui signifie :

  5 billes et 2 dés pèsent autant que 3 billes et 5 dés
  



• Traduire cet équilibre par une égalité dans laquelle apparaîtront m_b masse d'une bille
  et m_d celle d'un dé :

  5m_b + 2m_d = 3m_b + 5m_d
  



• Sur le plateau de gauche, Luc décide d’enlever les 2 dés ; que doit-il faire sur
  le plateau de droite pour que l’équilibre soit maintenu ?

  Enlever le même nombre de dés
  



• Traduire ce nouvel équilibre par une égalité et compléter le dessin :

  5m_b = 3m_b + 3m_d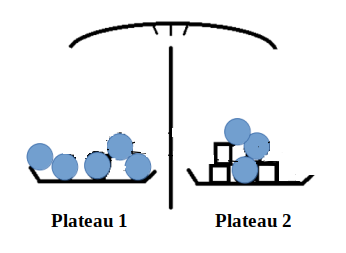
  
  
  



• Que devra faire Luc pour qu’il n’y ait plus de billes sur le plateau de droite
  tout en maintenant l’équilibre ?

  Enlever 3 billes sur chacun des deux plateaux
  



• Traduire ce nouvel équilibre par une égalité et compléter le dessin :

  2m_b = 3m_d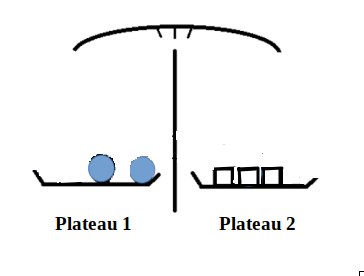
  
  
  



• Remplacer m_d par sa valeur (15) dans l’égalité précédente :

  2m_b = 3m_d  devient :
  2m_b = 3 × 15 => 2m_b = 45



• En déduire la masse d'une bille :

  m_b = 45 ÷ 2 = 22.5
  



• Nous avons résolu l'équation :

  5m_b + 2m_d = 3m_b + 5m_d
  



• Qui s’écrit, si on remplace md par 15 g :

  5m_b + 30 = 3m_b + 75
  



• En appelant x la masse d’une bille, on peut dire que nous avons résolu l’équation :

  5x + 30 = 3x + 75
  



• Vérification :

  Avec x = 22.5,
  5x + 30 = 5 × 22.5 + 30 = 112.5 + 30 = 142.5 et
  3x + 75 = 3 × 22.5 + 75 = 67.5 + 75 = 142.5
  
  142.5 = 142.5 donc une bille pèse bien 22.5 g